����������� ������������� ��������� 2001
����������� ��������� ��� �� ������������ ��������� - ����� 2�
�������: �� ������ ��� ���������� ��������� ��� ���� ����� �������� �������� ��� �����������. ���� ��� ����� �� ���������� �� ����������� ��� ���� �� �� ������ ��� �������� ��� ��������� ��������, ���� ��� �� ����������� (������ ��� �� ���������� � ��������) �� ������ ����������� ���� ����� ��������.
���������� ��������
1.
�� ![]() ����� ������� ���� ��������� ���� �������� �����
����� ������� ���� ��������� ���� �������� ����� ![]() ��
�������
��
�������
![]() .
������ ��� �������
.
������ ��� ������� ![]() ������ ����
������ ����
![]() ��� ����
��� ����
![]() .
.
2.
��
![]() ������������ �� ���������� ����� ��� �����������
�������
������������ �� ���������� ����� ��� �����������
������� ![]() .
��
.
�� ![]() ����� ������� ������ ��� �� ������
����� ������� ������ ��� �� ������
![]() ����� ����� ���
����� ����� ��� ![]() .
.
3.
� ��������� �����������
![]() ��������� ����
��������� ����
![]() ���������� ���
���������� ��� ![]() . ���� ��� ��� ���
. ���� ��� ��� ��� ![]() ����� ������ ���������� �������
���
����� ������ ���������� �������
��� ![]() .
������ ��� �
.
������ ��� � ![]() ����� ���������� ������� ���
����� ���������� ������� ��� ![]() .
.
4.
������ ��� �� ����� �� �����
![]() ���
���
![]() ��� �����
���������� ����� ���������.
��� �����
���������� ����� ���������.
5.
���� ![]() ����� �� ����� ���
����� �� ����� ���
![]() �������� ��������������. ������ ���
��
�������� ��������������. ������ ���
�� ![]() ����� �������� �� ��� ���� �� ����� ������� �� ������ ������
����� �������� �� ��� ���� �� ����� ������� �� ������ ������ ![]() .
.
6.
����
![]() ��������� �� ��� ��
��������� �� ��� �� ![]() ������ ����
������ ����
![]() , ��� �������� �������� ��������
, ��� �������� �������� ��������
![]() ��� ��� ��� ��
��� ��� ��� ��
![]() .
������ ��� �
.
������ ��� � ![]() ����� ���������.
����� ���������.
7.
���� ![]() ������ �� ������
������ �� ������ ![]() ���
��� ![]() ��� �� ����� ��
��� �� ����� �� ![]() � ��
� �� ![]() ���� �������� ��������� ��� ����� ��� ����������� �� ����� 5.
������ ��� ��
���� �������� ��������� ��� ����� ��� ����������� �� ����� 5.
������ ��� �� ![]() ���� ����� 0.
���� ����� 0.
8.
���� ![]() ������ ������� �������. �������� �� �������� ��� ��������� ���
������ ������� �������. �������� �� �������� ��� ��������� ���
![]() ,
, ![]() , �� �� supremum ��� �����������
, �� �� supremum ��� �����������
![]() , ��� ���
�� ����������� ���������
, ��� ���
�� ����������� ��������� ![]() ���
��� ![]() .
��
.
�� ![]() ����� �������������� ������ ���
����� �������������� ������ ��� ![]() .
.
9.
(�)
����
![]() ����������� ��������� ��� �������
����������� ��������� ��� ������� ![]() .
�������� ��� ��� ����
.
�������� ��� ��� ���� ![]() ,
� ����� ��o���������
,
� ����� ��o��������� ![]() ��� ��
��� �� ![]() �������� �����������
�������� ����������� ![]() ��������.
������ ��� �������� ����������� ��� ���
��������.
������ ��� �������� ����������� ��� ���
![]() .
(��������: ������� �� ����
.
(��������: ������� �� ���� ![]() - ���������� ��� ��������� ����
������
- ���������� ��� ��������� ����
������ ![]() ��� ��
��� �� ![]() ����� ����� �� �������
����� ����� �� ������� ![]() ��������.)
��������.)
(�) ������ ��� �� ���� ������ ��� ��� ������ ��������� �����������
������� ![]() , ��� ������� ��� ���� ������� ��� ��� ������� ������������
, ��� ������� ��� ���� ������� ��� ��� ������� ������������
![]() , ���
, ��� ![]() .
.
10.
��� ![]() �������� �� ������ ���������. �� ����� ��� ��� ��������
����������� ������� ������� ���������
�������� �� ������ ���������. �� ����� ��� ��� ��������
����������� ������� ������� ��������� ![]() ��� ��
��� �� ![]() ��� ���
��� ��� ![]() ?
?
���������� ��� �������� ��� ������� ���������� ���������
11.
��������� ��� � ����
![]() , �����
������� ���� ��� �� ��������
, �����
������� ���� ��� �� ��������
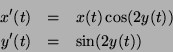
12. �� ������ � ������ ���� ��� ����������
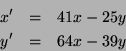
��������: ��� ((������� ����)) ������ �� ������ ��� �����
13.
��������� ��� � ���� ��� �����������
�������� �� ��� �� ��������
14.
�� ����� �� �������� �������-���������� �����
�� �� �������
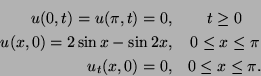
15.
�� ������ �������� ��������� ![]() ���� ���������
���� ���������
![]() ��� �� ����������
��� �� ����������
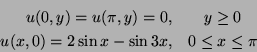
��� �� ����� ��������.
16. ��������� �� ����������� ��� ������ ������ ��� �����������
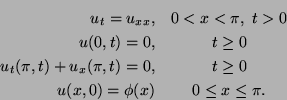
���������� ����������� ��������
17.
������ ��� � ��������� ![]() , ��
, ��
![]() ,
,
![]() ,
,
![]() , ��������� ��� �������� ������� ������ ��� ����������� ���
����������
, ��������� ��� �������� ������� ������ ��� ����������� ���
����������
![]() .
.
18.
���� ![]()
![]() ����������� ��� ������ ��������� �������,
���.
����������� ��� ������ ��������� �������,
���. ![]() ���
���
![]() ��� ���� �� �������� ��������
��� ���� �� �������� ��������
![]() .
.
(�) ������ ��� ![]() ,
, ![]() .
.
(�) ������ ���
![]() .
.
(�) ����� � ![]() ������ ���������?
������ ���������?
19.
���� ![]() ���
���
![]() ,
, ![]() , ���
, ���
![]() ��������� ���������� ���
��������� ���������� ��� ![]() ���
��� ![]() ,
, ![]() .
������ ���
.
������ ���
![]() .
.
20.
�� ����������
![]() ������ �� ������������ �� ��
������ �� ������������ �� ��
![]() ����
���� ![]() ��� ������ ����� ��������� ���
��� ������ ����� ��������� ��� ![]() ���
���
![]() �� ��������� ���������� ���
�� ��������� ���������� ��� ![]() ���
��� ![]() .
.
(�) ����� �� ![]() ��� ��������� ��� �������
��� ��������� ��� ������� ![]() ��� ���
����������� ����� ���
��� ���
����������� ����� ��� ![]() .
.
(�) ����� ������� ����� ����������� ����������� �������� ��� (�)?
21.
��������� �� ���������� ![]() ,
, ![]() ���
��� ![]() ���
�� ���������
���
�� ���������
![]() ,
,
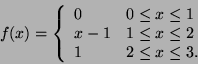
(�) ���������� ��������� ����������
(�) ���������� ��� ������ spline ����������
(�) ���� ��� ��� �������� ����� ������������
���������� �����������-�����������
22.
��� �����, ![]() ���
��� ![]() , ������� darts (�������) ��� � ������ ��� �� ����
������ ��������. �
, ������� darts (�������) ��� � ������ ��� �� ����
������ ��������. � ![]() ���� ����������
���� ���������� ![]() �� ���� ������ ���� ���� ���
������, ��� �
�� ���� ������ ���� ���� ���
������, ��� � ![]() ���� ����������
���� ���������� ![]() .
�� �� ������� ����� ���� ����������� ������ ����.
������ ��� ���������� �� �������� �
.
�� �� ������� ����� ���� ����������� ������ ����.
������ ��� ���������� �� �������� � ![]() ���� ����� ������ ������.
���� ����� ������ ������.
23.
���� ![]() ,
,
![]() , ��� ��������� ������ �������, ����������� ��� ��������
������� ���������� ��� ���� ���
, ��� ��������� ������ �������, ����������� ��� ��������
������� ���������� ��� ���� ���
![]() ���
���
![]() �������� ��� ����� ����������� ������� (��� ����
�������� ��� ����� ����������� ������� (��� ���� ![]() ).
��
).
��
![]() , ������ ���
, ������ ���
![]() .
(���������� ��� �����������
.
(���������� ��� ����������� ![]() ,
, ![]() ,
, ![]() .)
.)
24.
� ������� ������ ��� ������� ![]() ����� ��� � �����
����� ��� � ����� ![]() �����.
�� ������ ����� ����������� ������ ���� ��� �������� ������ �����
��� ������������ �������.
������ ��� ���������� �� �������� � �����.
�����.
�� ������ ����� ����������� ������ ���� ��� �������� ������ �����
��� ������������ �������.
������ ��� ���������� �� �������� � �����.
25.
(�) ������ ��� �������� ��� ����������� ![]() ����������� ������� ���������� ��
�������� Poisson �� ���������
����������� ������� ���������� ��
�������� Poisson �� ��������� ![]() ��� ��� �������. (� ������ ���������
��� ��� �������. (� ������ ���������
![]() ���� �������� Poisson �� ���������
���� �������� Poisson �� ��������� ![]() �� ������� �� ����
�� ������� �� ����
![]() �� ����������
�� ����������
![]() .)
.)
(�) ������ ���
26.
(�) �� ![]() ����� ��� ������ ��������� �� ����� ���
����� ��� ������ ��������� �� ����� ��� ![]() , ������ ���
, ������ ���
![\begin{displaymath}
{\bf E}\left[{N}\right] = \sum_{n=0}^\infty {\mathbf P}(N>n).
\end{displaymath}](img118.png)
(�) ����
������ ���
27.
�� ��� ������� ��������� ��� ������ ��� ![]() ����� ������� �� ����
����� ������� �� ���� ![]() ,
, ![]() ���
��� ![]() ��� ���� ������ �������� (genotypes)
��� ���� ������ �������� (genotypes) ![]() ,
, ![]() ���
��� ![]() ����������.
� ��������� ��� ��������
����������.
� ��������� ��� �������� ![]() ���� �������� �����
���� �������� �����
![]() ����
����
![]() ��� ������� ���������� �� ����� ���
��� ������� ���������� �� ����� ��� ![]() .
���������� ��� ����� ��� ����� ��������� ����� ����������� ��� ��� ��� �������
��� ���� ����� ����� ����������. ������ ��� ���������� �������� ������������� ���
.
���������� ��� ����� ��� ����� ��������� ����� ����������� ��� ��� ��� �������
��� ���� ����� ����� ����������. ������ ��� ���������� �������� ������������� ��� ![]() .
������ ������ ��� ���������� �������� ������������� ���
.
������ ������ ��� ���������� �������� ������������� ���
![]() ���
�������� �� ���� ����� ����������.
���
�������� �� ���� ����� ����������.
28.
(�) ������ ��� �� ![]() ���
��� ![]() ����� ����������� ��� �������� ������� ����������, �
���� ��� �� ��� ������ �������� ��������, ���� �
����� ����������� ��� �������� ������� ����������, �
���� ��� �� ��� ������ �������� ��������, ���� � ![]() ���� ��� �������� �������� ��
���������
���� ��� �������� �������� ��
��������� ![]() .
.
(�) ����
![]() ���
���
![]() ��� ���������� ������ ��������,
�� ����� ��� ��� �������� �� ��������
��� ���������� ������ ��������,
�� ����� ��� ��� �������� �� ��������
![]() ��� �� ������� ��� ���
�������� �� ��������
��� �� ������� ��� ���
�������� �� ��������
![]() .
������ ��� ���������
.
������ ��� ��������� ![]() ��� ��� ������� �����
��� ��� ������� ����� ![]() , ������ ���� ���� ��� ���
��
, ������ ���� ���� ��� ���
�� ![]() ���
��� ![]() �� ����� ��� 95% ������� ������������ ��� ��� ���������
�� ����� ��� 95% ������� ������������ ��� ��� ���������
![]() , �� ������ ���
, �� ������ ���
![]() .
���� ��� ��� ��� �������� ������������ �� ������������ ��� �������� ���
.
���� ��� ��� ��� �������� ������������ �� ������������ ��� �������� ���
![]() ��� �����?
��� �����?
���������� �������� - ����������
29.
(�) ���� �������� ����� ����� 143 ����� �������.
(�) �� ![]() ���
��� ![]() ����
���� ![]() ,
,
![]() .
.
(�) �� ![]() ����� ����� ������ �������
����� ����� ������ ������� ![]() ���
��� ![]() ������������
������ �� ���������� ��� �
������������
������ �� ���������� ��� � ![]() ����� � ����������� ������������ � �������������.
����� � ����������� ������������ � �������������.
(�) �� ![]() ���
��� ![]() ���
���
![]() , �� ���������� ��� ��� ����
, �� ���������� ��� ��� ���� ![]() ��� ����
��� ����
![]() ������
������ ![]() .
����� ���� ��������� �� ��
.
����� ���� ��������� �� ��
![]() ?
?
(�) �� ![]() ���
���
![]() ,
,
![]() , ���� ����� � ���� ���
, ���� ����� � ���� ���
![]() ?
?
30.
(�) ����� ��
![]() ����?
����?
(�) ����� ��
![]() ����?
����?
(�) ����
![]() . �� ������ ���� �����������
���
. �� ������ ���� �����������
��� ![]() ��� �� ��� ����� ������� ���
��� �� ��� ����� ������� ��� ![]() .
.
(�) ������ ��� ������� (maximal) ������� ��� ![]() .
.
(�) ������ ��� �� ���������� ������ ������� ��� ![]() ��� �� ��� ����� �����.
��� �� ��� ����� �����.
31.
(�) ����
![]() . �� ������ ��� ��������� �� ������ �����������
��� �� ����������� ���
. �� ������ ��� ��������� �� ������ �����������
��� �� ����������� ��� ![]() .
.
(�) �� ![]() ����������� �������� ������� ���
����������� �������� ������� ��� ![]() ������� ������� ���
������� ������� ��� ![]() ,
������ ����
,
������ ���� ![]() �� ������� ��
�� ������� �� ![]() , �� ���������� ��� ��
, �� ���������� ��� �� ![]() ��� ���� ����� ���
��� ���� ����� ��� ![]() .
.
(�) �� ![]() �������� ��� �������
�������� ��� ������� ![]() ���
��� ![]() ��������� �������� �� ���� �� ����
��������� �������� �� ���� �� ���� ![]() ,
�������� ������, �� ���������� ��� ��
,
�������� ������, �� ���������� ��� �� ![]() ����� ��������� ��������,
������ �������� ������ �� ���� ��
����� ��������� ��������,
������ �������� ������ �� ���� �� ![]() , ��� ���
, ��� ��� ![]() .
.
32. ������� ���� ���� ����� ��� 15 ���������, 20-������, 50-������, ��� 100-������. �� �� �������� ���� ���� 690 ������� ���� ��������� ���� ��� ���� �����?
33.
�� ������������ �� ����� ��� ����������
![]() ��� ����
��� ���� ![]() .
.
34. ��� �������� ��� ��� ����� ������� ����� �� ���� ��� ������ ��� �� ����� ����� �������� ������� ��� �� ����� ��� �� ��������� ����� ����� ������ ���� �����������. �� �������� ��� ����� ���������� ������ ���, �� ������� ���� 1 ������� ����������� ��� 7 ��� �� ������� ����� ����� ���������� ��� �� �������� ��� ������ ��� ��� �������� ���� 5. ���� ����� �� ���� ��� �� ����� ����?
35.
���� ���������� ���� �������� ![]() , ����
, ���� ![]() � ���������� ������,
���� � ����� �����������
� ���������� ������,
���� � ����� �����������
![]() (
(
![]() ).
�� ������� ��� � ����� ������ ����� ������������� �� �� ��������� �����.
).
�� ������� ��� � ����� ������ ����� ������������� �� �� ��������� �����.
36.
����
![]() � ��������� �� ����
� ��������� �� ����
���
(�) �� ������� ��� ��
(�) �� ������� �� ����������� ��� 1�� ��� ��� 2�� ����������� ������.
(�) �� ������������ �� ������ ������������, � ����������� Gauss ��� � ���� ����������� ��� ����� ������ ���
���� ��������. �. ����������, �. ������������, �. �������� ��������, 28 ������� 2001
����� �����������