����������� ������������� ��������� 2001
����������� ��������� ��� �� ������������ ��������� - ����� 1�
���������� ������������ ��������
1.
����
![]() , ���
, ��� ![]() (
(![]() �����
������� ��������).
�����
������� ��������).
�� ������ � ������� ���� ��� ![]() ��� ��� ������.
��� ��� ������.
2.
�������
![]() ��
��
����
3.
(�) ���������� ��
(�) ���������� ��
4.
(�) ����
![]() ������� ������ ���� ��� ���� ������
���������
������� ������ ���� ��� ���� ������
��������� ![]() �� ������
�� ������
������ ��� �
(�) ��
![]() �������,
�������, ![]() , ��� ��� ���� ������
���������
, ��� ��� ���� ������
��������� ![]() ��
��
![]() ������
������
�� �������� �� ����������� ��� ���
5.
���� ��������� ![]() ��
�� ![]() ���
���
��� ����
������ ![]() .
.
6.
(�) ����
![]() ��
��
![]() , ���
, ��� ![]() .
������ ���
.
������ ��� ![]() ������� ��� ���������� ��.
������� ��� ���������� ��.
(�) ������ ��� �������
![]() , ������������ ��� �����
������� ���, ���� �� ���
, ������������ ��� �����
������� ���, ���� �� ��� ![]() �� ����� �������� ���
�� ����� �������� ��� ![]() .
.
7.
����
![]() ��� �������� ���
��� �������� ���
����
������ ���
![]() .
.
���������� ��������� ��������
8.
(�) ��
![]() ��� ������� ��� ����
��� ������� ��� ���� ![]() ,
, ![]() ����� �� ������� ����
�� �������
����� �� ������� ����
�� ������� ![]() ���
��� ![]() ����� ������.
����� ������.
(�) ������ ��� (����������) �������
![]() �������� ���� ��
�������� ���� ��
![]() ���
��� ![]() �� ��� ����� ������.
�� ��� ����� ������.
9.
(�) �������
(i) ������ ���
(ii) �� ������ ��� ���� ��� � �������� ���
(iii) �� ������ ���� ���
(�) �� ������� �� �������������� ��� �������������
���
10.
�� ����� �� �������
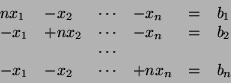
11.
����
![]() ,
, ![]() .
��
.
��
![]() ���� � �������
���� � �������
![]() �� ��������
�� ��������
![]() ,
,
![]() , ����� �����������������.
, ����� �����������������.
�� ������ ���� ��������� ������� ������ �� ��� ![]() .
.
12.
(�) �� ![]() ���
��� ![]() ����� ��� ������������� ���� ������������� �����
������������ ��������� ������ ���
����� ��� ������������� ���� ������������� �����
������������ ��������� ������ ���
![]() .
.
(�) ���� ![]() ����,
����, ![]() ����
���� ![]() -������������� ����� ���������
-������������� ����� ��������� ![]() ,
���
,
���
������ ����
(i) ������ ���
(ii) �� ���� �������� ��������� ������ � ������� ������ ���
���� ��������. �. ����������, �. ������������, �. ��������
��������, 27 ������� 2001
����� �����������